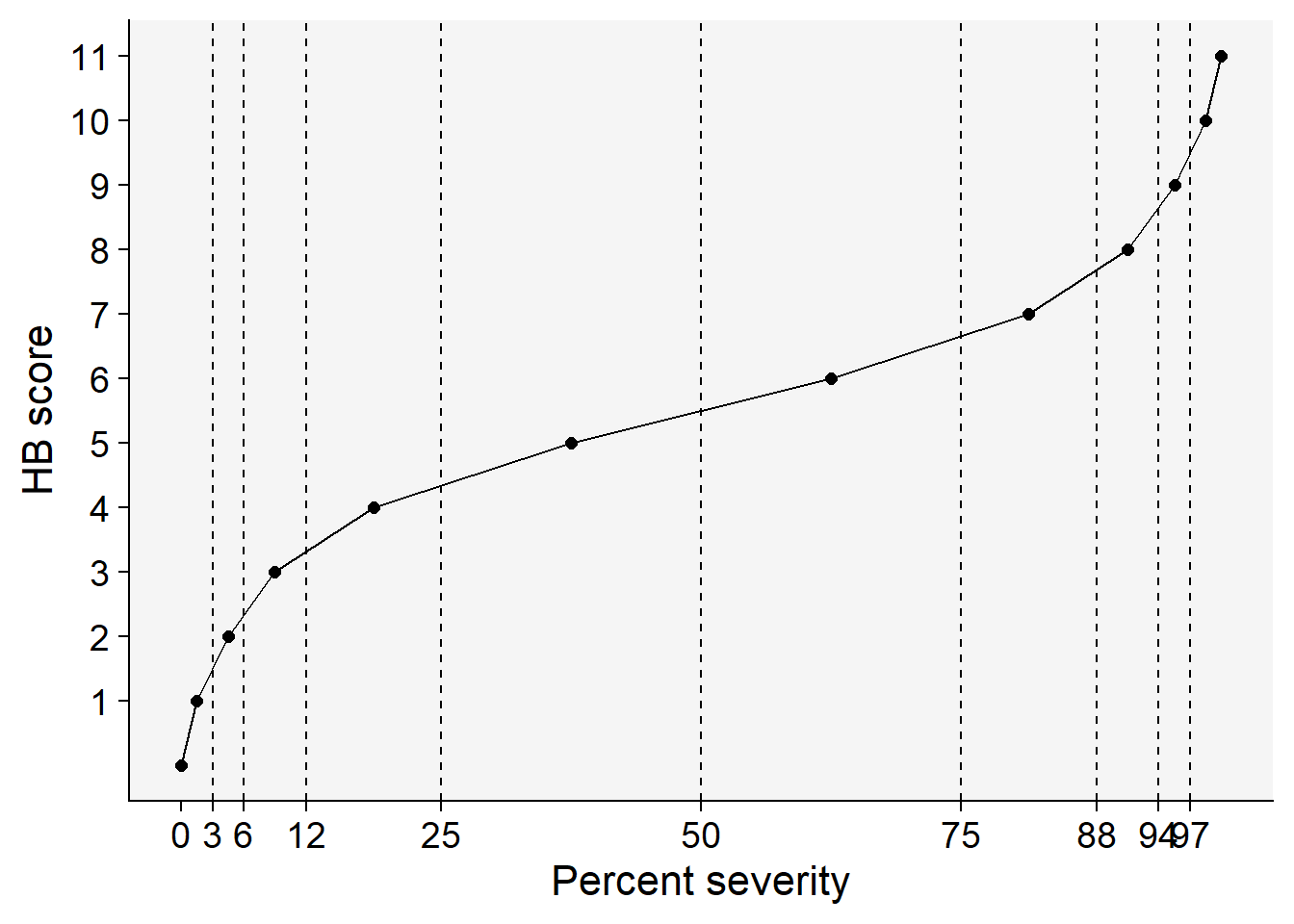
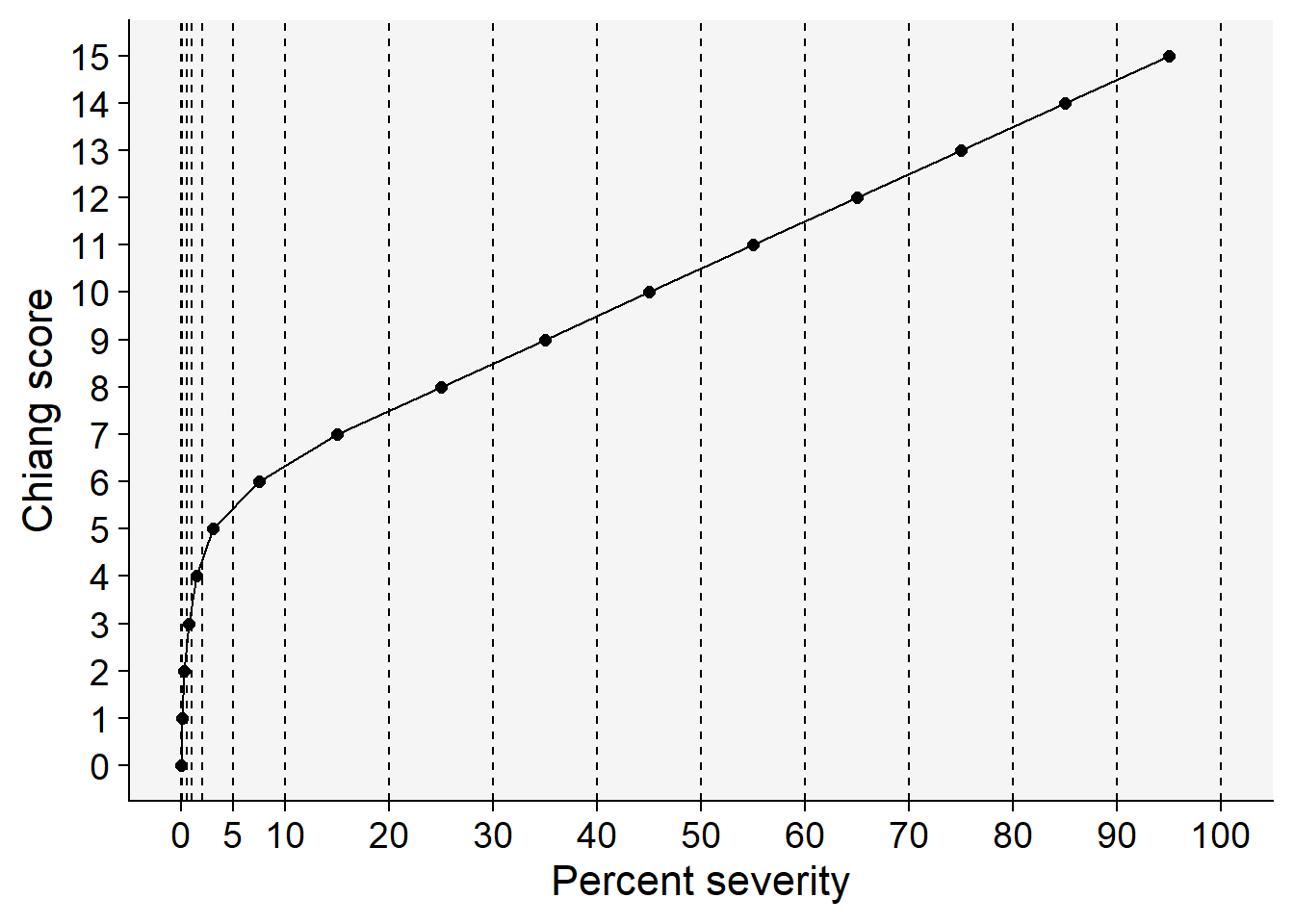
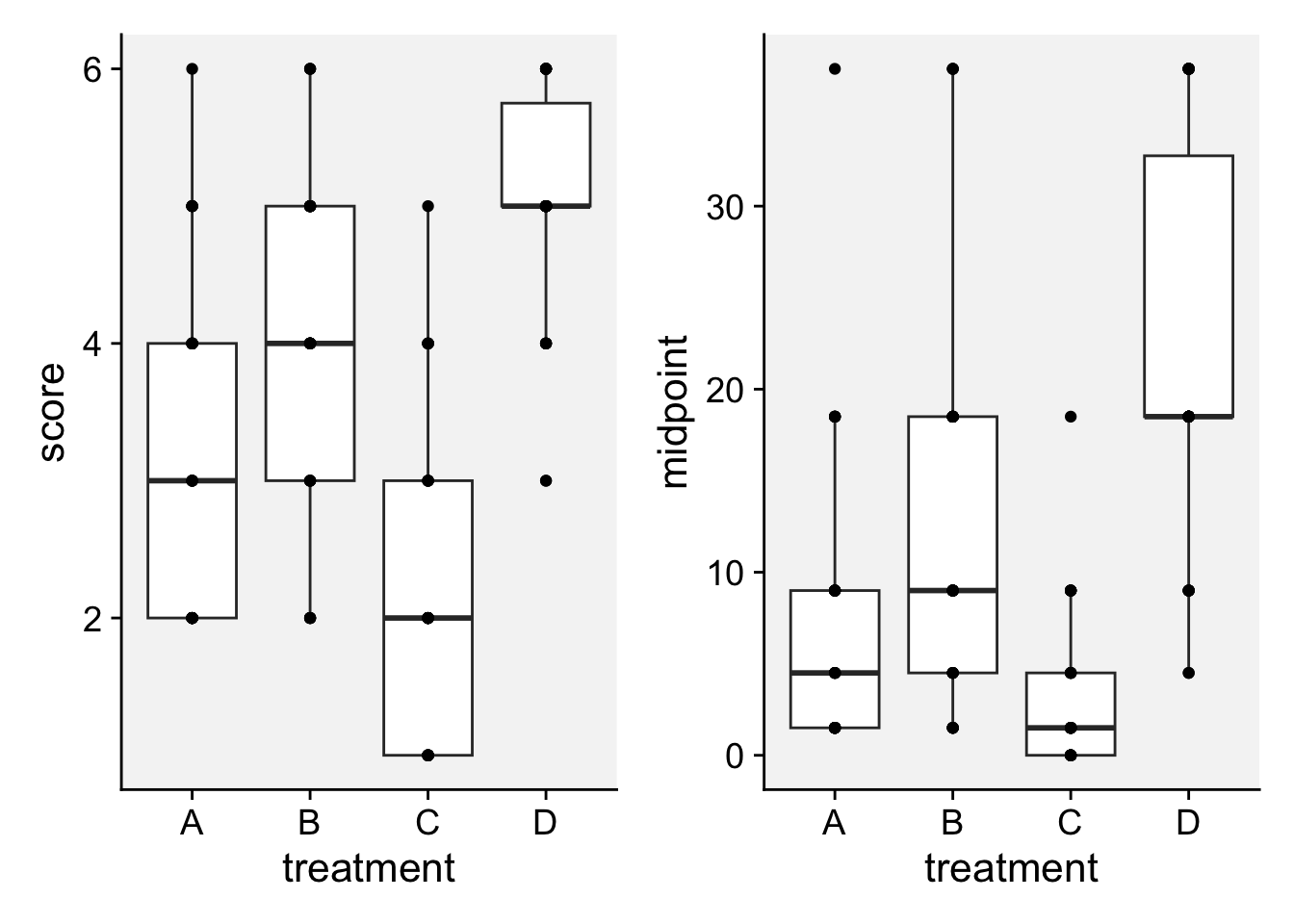
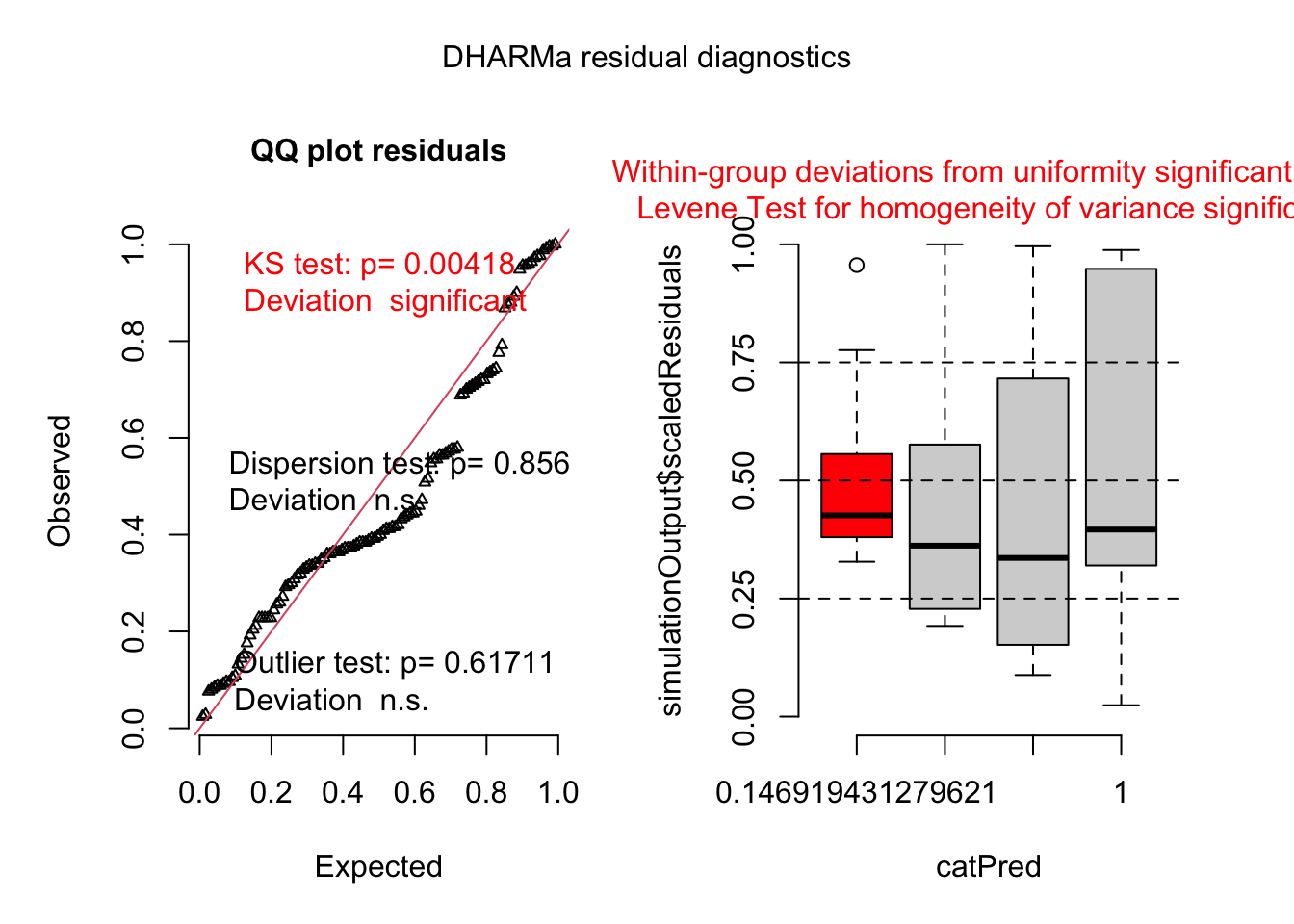
HB <- tibble::tribble(
~ordinal, ~'range', ~midpoint,
0, '0', 0,
1, '0+ to 3', 1.5,
2, '3+ to 6', 4.5,
3, '6+ to 12', 9.0,
4, '12+ to 25', 18.5,
5, '25+ to 50', 37.5,
6, '50+ to 75', 62.5,
7, '75+ to 88', 81.5,
8, '88+ to 94', 91.0,
9, '94+ to 97', 95.5,
10,'97+ to 100', 98.5,
11, '100', 100
)
knitr::kable(HB, align = "c")| ordinal | range | midpoint |
|---|---|---|
| 0 | 0 | 0.0 |
| 1 | 0+ to 3 | 1.5 |
| 2 | 3+ to 6 | 4.5 |
| 3 | 6+ to 12 | 9.0 |
| 4 | 12+ to 25 | 18.5 |
| 5 | 25+ to 50 | 37.5 |
| 6 | 50+ to 75 | 62.5 |
| 7 | 75+ to 88 | 81.5 |
| 8 | 88+ to 94 | 91.0 |
| 9 | 94+ to 97 | 95.5 |
| 10 | 97+ to 100 | 98.5 |
| 11 | 100 | 100.0 |